AI Memo #1(Efficiency Edition)
On the compressibility of Deep Learning Models (Large Neural Networks)
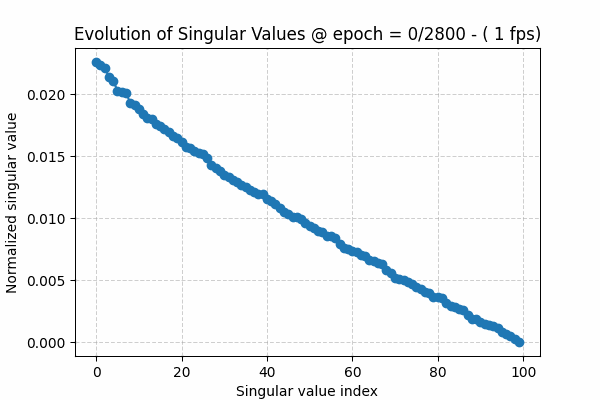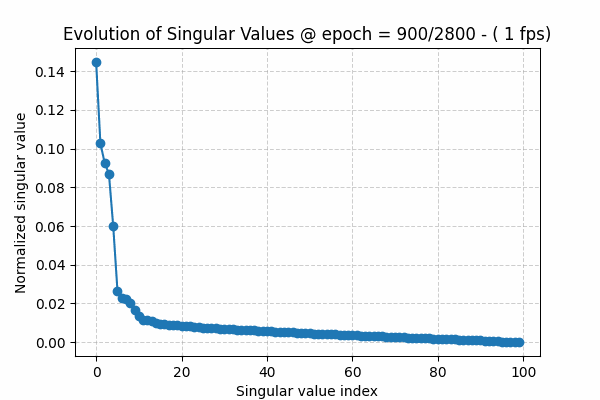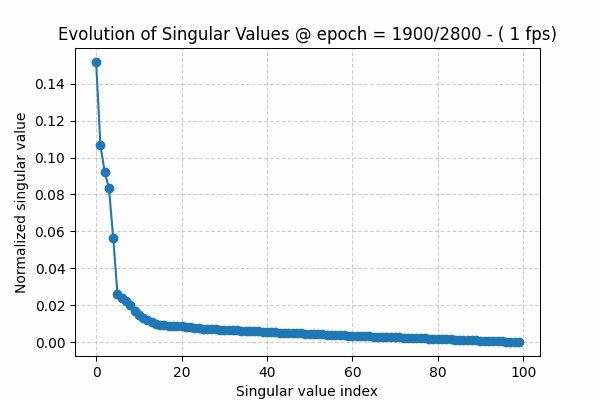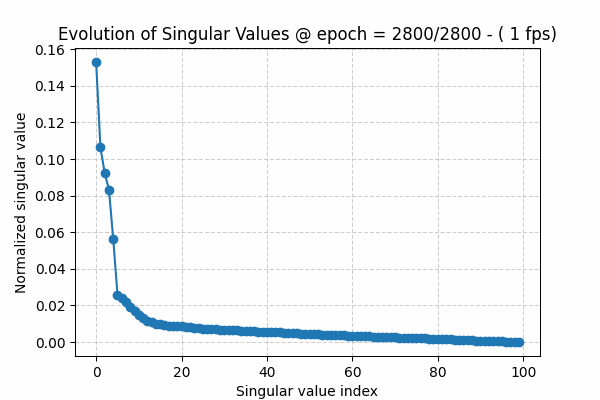
Table of Contents
Why reducing Neural Networks memory footprint is essential ?
Toy example showing the low-rank bias for neural networks
Further readings
Why is compressing Neural Networks essential for practical applications? (with examples)
One of the main barriers to adopting Large Language Models (LLMs) and large Deep Neural Networks in general is their large memory footprint. The two main reasons are:
Higher memory need: Larger models require larger clusters for deployment, which leads to higher running costs (that’s a no-brainer).
Higher inference time: When a model is deployed, the time needed for generating text (inference) is proportional to the number of parameters. Of course, this proportionality is not strictly linear, but parameter count is a strong indicator.
One of the active directions in Large Model development is leveraging the Low-Rank Approximation concept from linear algebra to reduce the number of parameters needed in each model layer [12][13].
In the context of LLMs, there has been huge progress in applying Low-Rank approximation to build models that are both smaller in parameter count and more efficient to fine-tune.
LoRA, a method developed by Microsoft Research, is a clear example of this direction. Compared to full fine-tuning of GPT-3 (175B), LoRA reduces the number of trainable parameters by a factor of 10,000, while still maintaining accuracy. This makes it possible to fine-tune LLMs with a much smaller memory footprint and lower compute requirements [15].
I will give a very shallow overview of the core idea of LoRA here, and will dig deeper into it in upcoming memos.
Before I proceed, you can a quick overview of what is Pre-trained models in [14]. Pretrained model is one of the fundamental technologies behind LLMs development.
During fine-tuning, the model starts from the pre-trained weights W0, which remain fixed, and applies an update ΔW as follows:
The key assumption is that these updates have intrinsic low rank. This means that intherintly the update matrix needs to have less number of parameters than the full matrix itself. This has been illustrated in LORA paper sec 4.1 [15].
The details of LORA approach is out of scope of this memo, however it tries to focus on the low rank-bias for neural networks (especially large ones).
Toy example showing the low-rank hypothesis for neural networks
To get a sense of what low-rank bias means for neural network, I have a created a toy example to train a 3-Layer neural network for a simple problem.
Problem : build a model for Y=tanh(Z), Z=AX , where Z,A,X are linear regression synthetic data generated using the make_regression sklearn method [8]
Train a simple Feed-Forward Neural Network (FFNN) with 3 layers over the dataset
Monitor the spectral distribution of the second layer weight , call it W2. Why second layer, because intuitively this the “free” layers the model latent parameters , free from input or output mapping .
The spectral distribution is simply the distribution of “normalized” singular values when applying Singular Value Decomposition (SVD) to a the weight matrix . SVD is a linear algebra approach for low-rank approximation [10]. The singular value distribution [11] can be written as\(s^*_j = \frac{s_j}{\sum_j s_j}, \forall j=1,2,..,\bar{r} \)where sj is jth singular value and r-bar is the full rank of a matrix (min of the 2 dimensions)
Layer # i (L_i) can be written as
\(Z_i = \sigma(W_iZ_{i-1}+b_i)\)
where sigma is a nonlinearity (tanh, sigmoid, RELU) etc… . Wi is the weight matrix and bi is the bias vector. [9]
The singular values of a matrix are ordered from largest to smallest, i.e. s1 ≥ s2 ≥ s3 and so on. During training, we usually see that at the beginning they decay slowly. As the algorithm converges, the spectrum shows a sharper decay: a few large values capture the underlying structure or signal, while the remaining values form the tail, representing noise.
To visualize this observation, I have created a gif showing this behavior over training epochs (Figure 1). The gif can be downloaded here. The source code for this toy experiment can be found here
Key Takeaway
All the low-rank approaches applied to Large Language Models, such as LoRA, are based on the following hypothesis: initially we have an over-parameterized model, but as the learning process proceeds, the true signal in the weights (captured by the larger, spiky part of the singular value distribution) starts to separate from the noisy tail. This allows low-rank methods to exploit this phenomenon, making the training or fine-tuning process more efficient.
Next Memo
In memo #2 I will start to dig deeper into LoRa and how it applies the low-rank hypothesis to make the model fine tuning process much more efficient. I will demonstrate that with a small toy example to show the core idea. Stay tuned !
Further Readings
If you are interested more in understanding the Low-Rank bias of Neural Networks and how the spectral distribution evolve during the models training, check refs 1 to 7
References
Galanti, T., Siegel, N., Gupte, A., & Poggio, T. (2023). SGD and weight decay provably induce a low-rank bias in deep neural networks. Center for Brains, Minds and Machines. Retrieved from https://cbmm.mit.edu/sites/default/files/publications/Low-rank%20bias.pdf
Feng, R., Zhang, Z., Xu, Y., Wang, W., & Zhang, Y. (2022). Rank diminishing in deep neural networks. Advances in Neural Information Processing Systems (NeurIPS 2022). Retrieved from https://proceedings.neurips.cc/paper_files/paper/2022/file/d5cd70b708f726737e2ebace18c3f71b-Paper-Conference.pdf
Pinto, J., Rangamani, A., & Poggio, T. (2024). On generalization bounds for neural networks with low rank layers. arXiv preprint arXiv:2411.13733. https://arxiv.org/abs/2411.13733
Idelbayev, Y., & Carreira-Perpiñán, M. Á. (2020). Low-rank compression of neural nets: Learning the rank of each layer. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2020), 8046–8056. Retrieved from https://openaccess.thecvf.com/content_CVPR_2020/papers/Idelbayev_Low-Rank_Compression_of_Neural_Nets_Learning_the_Rank_of_Each_CVPR_2020_paper.pdf
Zhao, H., Zhang, T., Chen, J., Schäfer, F., & Anandkumar, A. (2023). InRank: Incremental low-rank learning. arXiv preprint arXiv:2306.11250. https://arxiv.org/abs/2306.11250
Langenberg, B., Balda, E. R., Behboodi, A., & Mathar, R. (2019). On the effect of low-rank weights on adversarial robustness of neural networks. arXiv preprint arXiv:1901.10371. https://arxiv.org/abs/1901.10371
Kuzborskij, I., & Abbasi Yadkori, Y. (2025). Low-rank bias, weight decay, and model merging in neural networks. arXiv preprint arXiv:2502.17340. https://arxiv.org/abs/2502.17340
Sklearn make_regression
https://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_regression.htmlWeight and Biases in Neural Networks
https://www.geeksforgeeks.org/deep-learning/the-role-of-weights-and-bias-in-neural-networks/SVD (Book Chapter ) https://www.cs.cmu.edu/~venkatg/teaching/CStheory-infoage/book-chapter-4.pdf
THE EFFECTIVE RANK: A MEASURE OF EFFECTIVE DIMENSIONALITY
https://www.eurasip.org/Proceedings/Eusipco/Eusipco2007/Papers/a5p-h05.pdfCS168: The Modern Algorithmic Toolbox
Lecture #9: The Singular Value Decomposition (SVD)
and Low-Rank Matrix Approximations
Tim Roughgarden & Gregory Valiant∗
April 30, 2024
https://web.stanford.edu/class/cs168/l/l9.pdf
Demystifying Neural Networks: Low-Rank Approximation
The Art of Matrix Factorization
https://medium.com/@weidagang/data-compression-with-low-rank-approximation-using-neural-networks-d6a8e8426101
What is a pretrained model? https://www.ibm.com/think/topics/pretrained-model
LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS https://arxiv.org/pdf/2106.09685