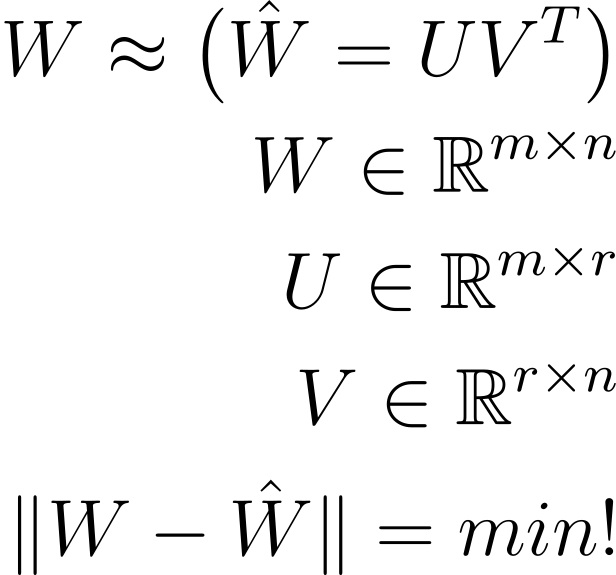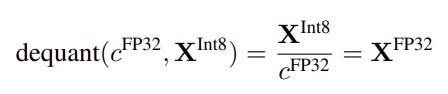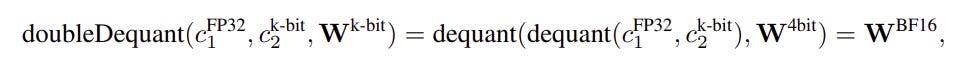Handling the curse of size in LLMs
Low-Rank Approximation and Quantization
What to expect in this article:
In simple words : what is low-rank approximation for Deep Learning
How Low-Rank benefits Large Language Models Practically
Example Models : Lora - QLora - AdaLora
Low Approximation for Deep Learning
The Problem : One of the practical bottlenecks for large deep learning is size (yes , size matters in these cases).
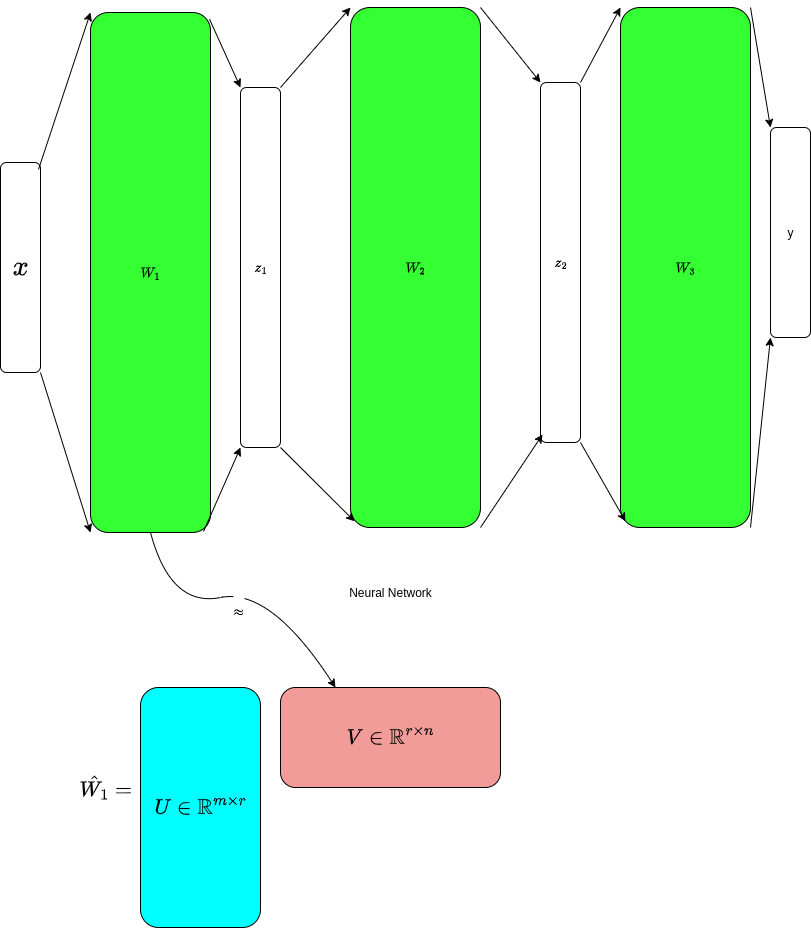
One mathematically sound approach is to to find a low-rank approximation (i.e. less in size) to the neural network weights with minimal loss of information. This can be formulated as follows:
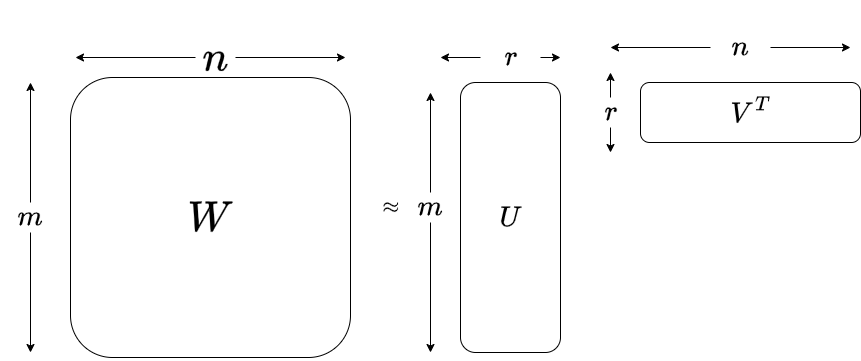
So what does this nice equation and figure say ? It says we will approximate a “fat” matrix (W) of size mxn by two (thin) matrices U and VT of sizes mxr and rxm (where the real rank of W r’ is larger then the approximation rank r .
For this low rank approximation to be effective as a compression too , (mxr)+(rxn) must be significantly smaller than (mxr). For more information about Low-Rank matrix approximations, see related link #1 below.
So how Low-Rank approximation is useful in the context of Deep Learning ?
It is a mathematically principled for compressing models with minimal loss of accuracy .
More precisely , Low-Rank approximation is applied to some model weights
(usually the large ones).
How low-ranking is applied to Deep-Learning models , well there is 3 general categories of approaches
Pre-Train methods : This is simple training a model via vanilla methods (Gradient Descent and its variants) then find Low-Rank approximation (via SVD or so) .
Another way is to use Low-rank reconstruction approach , like reconstructing using SVD outputs (W’ = U.S.VT) , and use this low-rank reconstruction as a warm initial state for re-training.
Pre-Set : these methods “force” low rank architecture when training the model from scratch. This is by replacing W by the low rank parts U,VT during the training process itself.
Compression-aware : These methods usually work by modifying the objective function for training to have a penalty term to make the training process prefer matrices with low-rank architecture.
This is a hot topic in Deep-Learning which needs dozens of articles to talk about.
If you are interested in more details, check related link #2
Low-Rank approximation and Large Language Models
In this article, we will just scratch the surface of two approaches that applies Low-Rank approximation (along with anther memory-saving technique called Quantization) to show how the memory footprint along with fine tuning and inference can be optimized dramatically for Large Language Models.
Meet LoRa : Low-Rank approximation for LLMs . This is a model developed by Microsoft researchers that achieved 10,000X reduction in number of trainable parameters (yes, you have read that right) and 3X reduction in GPU memory requirements (only 3X :))
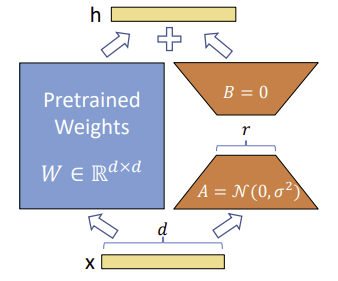
The core ideas is simple , the training for the model is on 2 phases : base-model training to have the pre-trained model and the task-specific training . The magic happens at the task-specific training phase (you can call it fine-tuning)
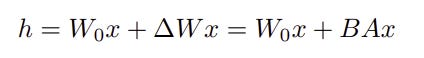
Let the W0 be the weight for the pre-trained or base model. During the gradient descent phase for the task-specific training , using W0 as an initial state , the delta_W (change in weight by calculating the partial gradient of the loss function relative to the weight), is assumed to follow a low-rank structure. Let W0 be of size d x k, then B of size d x r and A of size r x k, with r << min(d,k). For more details see relevant link # 4,5.
This formula is based on the general hypothesis that in “later” stages in training neural networks, the delta of weight follow low rank structure as the spectral distribution of weights becomes more dense . For more details see related link #5, 6, 7.
QLoRa tries to go an extra mile by applying “Quantization” to LoRa . You can think of quantization is another kind of “information compression” : it converts a variable from a higher precision data type that spans a wide range (like float32) to a smaller size lower precision data type like (Int8).
The main idea is that during training, weights parameters tends to converge to a “compressed” range that makes this kind of quantization poissible
Quantization operation from Float32 (4 bytes) to Int8 (1 byte) which makes a 4x memory compression can be formulated as follows:
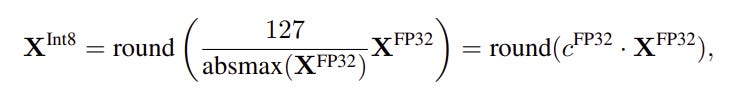
and reverse operation “De-Quantization” or “Dequant”
Give these two operations , the quantization (and dequantization) operations in Fig 4 and 5 are applied to the low-rank updates in figure 3 as follows
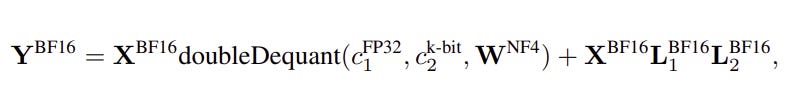
Where
BF16 : Is the Brain floating point data type from Google that compress memory but keep an acceptable float range
NF4 : is a 4-bit normal float , which is a data type that is optimized to for quantizing normally distributed variables
doubleDequant : is a defined operation to apply dequantization twice for data
This kind of quantization leads to a significantly smaller model memory footprint and more efficient fine tuning while keeping comparable accuracy.
For more information about QLoRa and how it works , check related link # 8.
In this article I tried to give a quick overview about to main “efficiency boosters” for LLMs : low rank approximation and Quantization . In next articles I will try to dig deeper in these concepts along with some experimentation.